Sequence and Series Questions are gaining importance in competitive exams be it for IBPS Clerk, PO, RRB, SO, or SBI Clerk or PO. The number of questions and the complexity of questions vary from exam to exam every year.
Sequence and Series questions are complex in nature and require an understanding of Numbers Systems, Squares and Square roots, Cubes and Cube roots, Math Tables, and other types of Arithmetic and Geometric Series are given in this article.
In this article, you’ll also find Examples of Sequence and Series Questions and Practice on Sequence and Series Questions.
Nowadays, questions in exams are mixed of multiple series and it requires practice and a deep understanding of basic concepts along with quickly identifying numbers.

Table of Contents
What is Sequence?
A sequence is a collection of numbers that is in order. In other words: a sequence is a list of items, objects, or numbers that are arranged in sequential, linear, or any custom order.
In sequence, each number is separated by a comma and is enclosed within curly brackets ‘{}’ also called set brackets. For example: {a1, a2, a3, a4, …}. A number such as 1, 2, 3, 4, … represents the position of that number.
There are two types of sequences: The Finite sequence and the Infinite sequence.
What is a Finite Sequence?
When any sequence is having a limited number of items, objects or numbers is called a Finite Sequence. For Example: {a1, a2, a3, a4} or {1,3,5,7}
What is Infinite Sequence?
When any sequence is not having a limited number of items, objects or numbers is called an Infinite Sequence. For Example: {a1, a2, a3, a4, …} or {1,3,5,7, …}
Properties of Sequence
Notation of Sequence
Sequence Notation is a way of representing a sequence, each number is separated by a comma and is enclosed within curly brackets ‘{}’ also called set brackets. For example: {1, 3, 5, 7}.
Rule of Sequence
The sequence follows a Rule which means that every number is having a common rule in which every number follows. For example, a sequence {3, 5, 7, 9}, so as per Rule we can see that there are 2 number differences between every number.
This sequence can be said to be incremental by 2 for each number. If we’ve to add a new number to this sequence then as per Rule we’ll add 2 to the last number and the new number will be 9 + 2 = 11.
Rule as a Formula
These rules can be simplified in mathematical expression or formula as 2n + 1. This expression can be tested by putting n numbers and checking if the sequence follows the rule or not. With the help of expression, we can find 100 elements.
100th Element in Sequence can be found by applying the above formula which is 2 x 100 + 1 = 201.
Finding Difference
Many times it’s easier to find the difference between two consecutive numbers. These differences are in such a way that it becomes simpler to understand the construction of that sequence.
From the above example, we found that there’s a difference of 2 numbers in every consecutive number hence it became simpler to understand. Also, it helps to find the next number or n(th) number.
Sometimes differences cannot be easily found at the first level then we need to analyze the difference and understand whether it’s forming another series. For example: {2, 4, 7, 11, 16, 22, …} from this example we’ll create another sequence of differences as {2, 3, 4, 5, 6, …}. Now from this level, it’s clear that the difference between every number is 1.
As per the above example if we have to find out the next number in this sequence then we’ll find the next number of different sequences, that is 6 + 1 = 7. Now actual number of the sequence is 22 + 7 = 29.
What is a Series?
The sum of an Infinite sequence is known as a Series. It looks similar to a sequence but the series has a plus sign (+) between its numbers. For example Series is denoted as: SN = a1+a2+a3 + .. + aN.
If the sequence is Finite or Infinite, it’s called a Series only when it’s not summing all numbers. If we sum up a few numbers in sequence then it’s called a Partial Sum.
Difference between Sequence and Series Questions
Below are the difference between sequence and series questions:
| Sequence | Series |
| Numbers in sequence follow a pattern. | Sum of numbers in the sequence. |
| The sequence has a Rule. | Series can have Rule. |
| The order of numbers is important. | The order of numbers is not so important. |
| Finite sequence: 1, 3, 5, 7 | Finite Series: 1 + 3 + 5 + 7 |
| Infinite sequence: 1, 3, 5, 7, … | Infinite series: 1 + 3 + 5 + 7 + … |
Types of Sequence and Series Questions
Below are the different types of Sequence and Series Questions, which are commonly asked in Bank Exams.
Odd Number Sequence and Series
The number in this sequence and series are odd numbers. The start of a series can be from any odd number and all the numbers in a series are odd numbers. This odd number sequence and series can be finite or infinite. For example: {5, 7, 9, 11, …}
Even Number Sequence and Series
The number in this sequence and series even numbers. The start of a series can be from any even number and all the numbers in the series are even numbers. This even number sequence and series can be finite or infinite. For example: {4, 6, 8, 10, …}
Arithmetic Sequence and Series
In Arithmetic sequence and series, every element or next number is formed by adding or subtracting a definite number from the preceding number. For example: {a, a+d, a+2d, a+3d, … }
In the above example, ‘a’ is the first term, and ‘d’ is the difference between two consecutive terms also known as common difference. Note: ‘d’ cannot be zero else all numbers will be the same as ‘a’. For example: {a, a, a, a, …}.
Geometric Sequence and Series
In Geometric sequence and series, every element or next number is formed by multiplying or dividing a definite number by the preceding number. For example: {a, ar, ar2, ar3, … }
In the above example, ‘a’ is the first term and ‘r’ is the factor between two consecutive terms also known as a common ratio. Note: ‘r’ cannot be zero else series will have only one number as ‘a’. For example: {a, 0, 0, 0, …}.
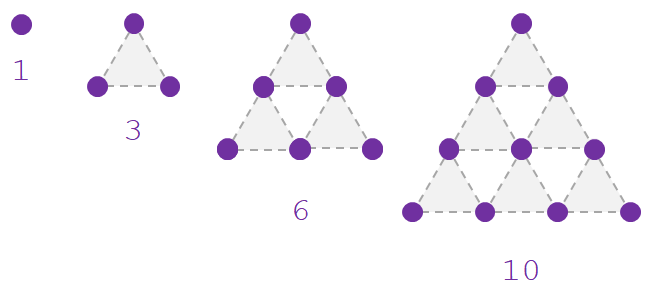
Triangular Sequence and Series
Triangle is formed from a pattern of dots, and these dots form triangular sequences and series. By adding a new row of dots and counting all the dots of the triangle, we can find the next number of the sequence. Triangular sequence and series follow the below formula:
xn = n(n+1)/2
Fibonacci Sequence and Series
Fibonacci sequence and series form an sequence of numbers in which each number is obtained by adding two preceding numbers and the sequence starts with 0 and 1. Sequence is defined as, F0 = 0 and F1 = 1 and Fn = Fn-1 + Fn-2. For Example: 0, 1, 1, 2, 3, 5, 8, 13, …
Other Sequence and Series Questions
Above mentioned sequence and series questions are the common and widely used ones. However there any many other types of series that can be formed using Squares and Square roots, Cubes and Cube roots, and Math Tables. Any custom type of sequence can also be formed, but the approach to solving them remains the same by finding a rule.
Solved Example on Sequence and Series Questions
Below are the solved examples on the sequence and series Questions:
Example 1: 5, 8, 13, 21, 34, n. Find the value of n?
Solution 1: From the above sequence, it’s clear that this is the Fibonacci series. For finding the value of ‘n’, as per Fibonacci we need to sum up the previous two numbers: 21 + 34 = 55.
Example 2: 216, 343, 512, 729, n. Find the value of n?
Solution 2: From the above sequence, it’s clear that this is a cube series.
For finding the value of ‘n’, we need to find the cube root of 729, which is 9. Now next number in the sequence is a cube of 10. So the final answer is 1000.
Example 3:25, 36, 49, 64, n. Find the value of n?
Solution 3: From the above sequence, it’s clear that this is a square series.
For finding the value of ‘n’, we need to find the square root of 64, which is 8. Now next number in the sequence is a square of 9. So the final answer is 81.
Example 4: 16, 19, 22, 25, n. Find the value of n?
Solution 4: From the above sequence, we’ll find the difference between all numbers and it’s having a common difference of 3. So value of n is 25 + 3 = 28. Also, the above example is of Arithmetic Sequence and series.
Example 5: 9, 27, 81, 243, n. Find the value of n?
Solution 5: From the above sequence, we’ll find the ratio for all numbers and it’s having a common ratio of 3. So the value of n is 243 x 3 = 729. Also, the above example is a Geometric Sequence and series.
Practice Sequence and Series Questions
Below are some Sequence and Series Questions to practice:
- Find the value of n in sequence: 23, 28, 33, 38, n?
- Find the value of n in sequence: 19, 27, 35, 43, n?
- Find the value of n in sequence: 21, 18, 15, 12, n?
- Find the value of n in sequence: 1, 2, 5, 10, 17, n?
- Find the value of n in sequence: 1, 8, 9, 64, 25, n?
- Find the value of n in sequence: 18, 54, 162, 486, n?
- Find the value of n in sequence: 2, 4, 10, 20, n?
- Find the value of n in sequence: 10, 5, 2.5, 1.25, n?
- Find the value of n in sequence: 6, 10, 16, 26, n?
- Find the value of n in sequence: 1, 2, 9, 64, n?
FAQs on Sequence and Series Questions
What are Sequence and Series?
A sequence is a collection of numbers that is in order. A Series is a sum of a given sequence.
Different types of Sequences?
Sequence are of two types: Finite sequence and Infinite sequence. Example of Finite sequence is: {1,2,3,4} and Infinite sequence: {1,2,3,4, …}
Common Sequences?
A few common sequences are Arithmetic Sequence, Geometric Sequence, Square Numbers, Cube Numbers, Fibonacci Series, and many others…
What is a Finite Sequence?
If the sequence is having finite or limited numbers, then that sequence is called a Finite Sequence. For Example: {1, 2, 3, 4, 5}, this sequence is having only 5 numbers.
What is Infinite Sequence?
If the sequence is having infinite or unlimited numbers, then that sequence is called an Infinite Sequence. At the end of numbers, there’s a continuation sign ‘…’. For Example: {1, 2, 3, 4, 5, …}, this sequence is having infinite numbers.
Final Words
Practicing the above questions for Sequence and Series Questions is not the end of your practice, but it’s a start of a new journey to apply logic to Sequence and Series Questions solutions with multiple approaches in right and faster way.
For cracking competitive exams one must practice Sequence and Series Questions without a calculator is a must. At last, during the exam, if a solution for Sequence and Series questions cannot be found easily then mark that question to revisit and move ahead instead of wasting time and energy.

